A formula for iterating the nth polygonal number is below. In the formula below a is herewith denoted to be greater than zero. For A=1 one gets the triangular numbers, a=2 the square numbers, and so on. This formula was derived when the author observed that the triangular numbers can be represented by the sum of x numbers of the form x+1 with x>= 0. He then carried out the experiment further and discovered every polygonal number may be represented as the sum of x numbers of the form ax+1 where x is greater than or equal to zero.
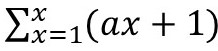
Unfortunately for the author this formula of his was a rediscovery.
Links below where this formula is discussed.
http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Figurate/figurate.html#section4.1
http://mathshistory.st-andrews.ac.uk/Biographies/Hypsicles.html
My Mathematics work and other extraneous diversions 